OpenSeaMap-dev:En:Depth Data
This Page describes the necessary efforts to retrieve and analyze depth data as well as create renderings from it
Inhaltsverzeichnis
Data Aquisition
Depth data can be retrieved from public domain sources or from crowd sourced data.
GEBCO
DIe Daten sind gerendert und stehen als Layer zur Verfügung:
| Zoom | Inhalt |
|---|---|
| 0..10 | Blaustufen und Schattierung |
| 11..18 | beschriftete Tiefenlinien, Blaustufen und Schattierung |
Noch zu lösende Probleme:
- der GEBCO-Layer erzeugt einen milchigen Schleier über der Basiskarte
- Tiefenlinien sind ab z=14 etwas grob (also ab da, wo dann die Flachwassertiefen beginnen) [1]
- Überschneidungen von 100m-Linie und Küstenlinie [2]
- Steilküsten (Cuba) [3]
Crowd Sourced Data
Crowd sourced data may be gathered by YOU. There are two options in development. A hardware and a software option.
Hardware logger
We are currently developing a hardware logger that may easily be plugged to the ship's network in order to log the networks data to a SD card. That data may then be uploaded by plugging the SD card to a normal computer with internet connection for upload. The main goal is to support NMEA 0183 data with options for NMEA 2000.
Software logger
A Software logger is in development and can be retrieved here.
It currently supports:
- Bluetooth
- serial ports
retrieving NMEA 0183 data (Bridge needable)
IP Support and NMEA 2000 development is underway.
Upload Process
You'll find further information here.
Data Preprocessing
Data Condition
Raw data is usually erronous and must be corrected
Internal data problems
Depth data may be affected by electrical conditions and software implementations
- Data is incomplete and fail their checksum (bus errors from physical transmissions errors)
- Data is erronous sensor data
- Approximate correctable data i.e. invalid GPS position that may be interpolated
- Uncorrectable data i.e. failed log sensor that shows slow speeds
- Data resolution is low i.e. for energy saving purposes GPS position is updated every 10 seconds instead of every second
- Sensor data is actively miscalibrated i.e. charter companies add additional draft to the sensor depth for safety reasons
External data problems
Depth data may be affected by different environmental circumstances
- The water temperature affects the ultrasound echo. An inhomogen water temperature yields unwanted echos
- The seabed affects the ultrasound echo
- The seastate affects the measurement. There even may be waves when there is no wind.
- Waves may affect the roll of the measuring vessel resulting in steep measurements that are invalid.
- The sounder sensor is not the position of the GPS antenna. A position offset including heading must be incorporated.
- The time of the measurement need not correlate with the time the position was received. This may even happen due to processing time of the hard or software.
Solution Proposal
Outline
The ship is influenced by the outlined environment which can be observed. Naturally what is observed is not the state of the ship as i.e. the position if taken from GPS is 95% less than 10m accurate. To improve quality an estimation of the true state yields better results if this noise taken into account properly.
Details
The ship moves according to physical laws. For the easist case imagine a ship with constant velocity and direction. For any point in time you can tell where the ship is with easy math. Considering the full blown setup a ships movement is affected by many parameters such as wind speed, water current, waves, tide, and many more. The ship moves also triaxial in a dynamic way in itself (roll, pitch, yaw). Heeling even changes the measurement position with respect to the depth position. In terms of a filter this is called a system model that describes how the state of the ship may change. Given such a state you can measure what your sensor readings are and compare that to where the system thinks you are.
The Kalman Filter is known to be the best linear estimator for such situations. Unfortunately the system model is not linear which is why the Extended Kalman Filter needs to be used in order to linearize the system at hand.
Todo:
- Construct ship system model with at least the position state and probably its course and speed or even more (depth)
- Estimate the system variance (This is a hard one, proposals welcome)
- Construct the measurement model according to the data available (GPS, Log)
- Estimate the measurement noise according to specifc sensors (DPGS is more accurate than GPS)
The estimation with the position and depth can be retrieved and stored in a database.
Pitfalls:
- If the system noise is badly chosen the estimation of the system state does not converge to the true state / measurement.
- If the system is very detailed the system variance can be reduced. The required cpu time for processing increases
Benefits:
- Having the best estimation of the true position even if measurements are noisy
- Easy and effective algorithmic processing
Analysis
Data Sets
Currently two test data sets are available recorded during trips from Mallorca and the Baltic Sea. In terms of data quality the Mallorca data shows many challenges.
- The minimum recommended sentences from NMEA showed up with false date and time readings while having correct (!!!) message checksums.
- The log on the ship was defective and delivered no readings from time to time.
- The same holds true for the water temperature.
- The GPS positions relatively imprecise because some last decimal digits are missing in the recordings.
- The GPS positions are updated every 10 seconds while other sensor readings update almost every second.
- The GPS position are sometimes way off due to false readings
The Baltic Sea data set is a little bit better
- Only a single day is available
- GPS positions are updated every second
One problem with the data is that there is time available when sensor readings were recorded. This yields problems to the filter algorithm.
Filter Algorithm
At first the Extended Kalman Filter is being analyzed. Using an apache implementation with the available data the filter quickly throw an exception that a matrix is not invertible because of numeric instabilities. When removing this exception the filter seems to work but the removal and its effects have yet to be analyzed. Literature suggest that a fixed interval smoother may yield better results in case of offline data processing. As it is an extension to the existing kalman filter we may consider that for the future.
One problem are the different update rates of the sensors. As GPS may deliver positions at 0.1Hz speed is updated at 1Hz. Literature suggests that the missing measurements shell be modelled as a random variable with the standard deviation of the sensor. It may even be possible to update covariance matrices only partially with the sensor readings received. Input for the best solution may be formulated on the developer mailing list.
Results
A prototype implementation is shown in the following screenshots. An Extended Kalman Filter is being used. It has the position and the current bearing and velocity as system state. The input is the measurement of these four observables. The system function is good old pythagoras. In a first implementation I tried to use orthodrome distances but the system function is not differentiable which is a requirement of the Extended Kalman Filter (due to acrtan2). For small distances pythagoras should be sufficiently accurate. The initial state is taken from the first measurement for convergence reasons.
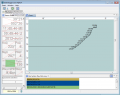
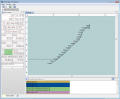
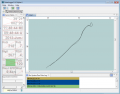
The following gallery shows the results.
- You can see the bad position resolution and an outlier in the first screenshot.
- The second shows the same data overlaid with the applied filter. The outlier is gone and the resolution has improved.
- The third screenshot shows data from a different GPS sensor with more precision (not DGPS) versus the filtered data.
This of course is just a preliminary test and many setups need to be considered to make it work for most datasets.
The overall process even gives an estimation of the current error which is a capability of the Kalman Filter. This way positional inaccuracies may be added to the overall depth measurement inaccuracy.
Quality rating
Each record (time, positon, depth) should become a quality rating.
Points
Derived from the Fibonacci series.
| Point | Description |
|---|---|
| 1 | extra small improvement |
| 2 | small improvement |
| 3 | medium improvement |
| 5 | large improvement |
| 8 | extra large improvement |
Factors
| Name | Factor | Description |
|---|---|---|
| depth offset | 8 (extra large) | The difference between the depth measured by the echo sounder and the depth (waterline) measured by hand. |
| device distance | 3 (medium) | The distance between gps antenna and echo sounder (lengthwise and crosswise). |
| SBAS | 3 (medium) | Satellite based augmentation system (WAAS, EGNOS, MSAS) which allows to correct the gps position. |
| position interpolation | 2 (small improvement) | Arrival of depth and position packets can have a time difference. It is/should be possible to interpolate the position. |